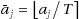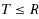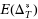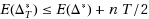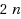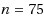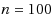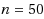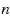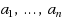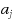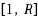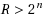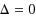Lattice‐based algorithms for number partitioning in the hard phase

We propose reductions of the NPP and the BalNPP in the hard phase to the closest vector problem (CVP). We present a binary search algorithm that solves the original problems by making polynomial numbers of calls to a CVP oracle. Second, we propose a truncated NPP algorithm, which finds approximate minimum discrepancies. In place of the original instance, we solve a modified instance with 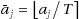${\overline{a}}_j=\lfloor a_j/T\rceil$ for some 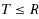$T\le R$ . We show that the expected optimal discrepancy of the original problem given by the truncated solution, 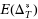$E\left({\Delta }_T^{*}\right)$ , is not much different from the expected optimal discrepancy: 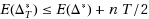$E\left({\Delta }_T^{*}\right)\le E\left({\Delta }^{*}\right)+nT/2$ . Third, we propose a direct mixed integer programming (MIP) model for the NPP and the BalNPP. We solve a lattice‐based reformulation of the original MIP model using standard branch‐and‐cut methods. Based on these results, we propose computational techniques that are efficient in practice. In place of the binary search, we implement a discrete search heuristic that applies basis reduction (BR) to several CVP instances (fewer than 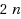$2n$ in most cases). This method finds near‐optimal solutions without proof of optimality to NPP problems with reasonably large dimensions, up to 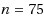$n=75$ . The truncation algorithm can be used to find good quality partitions within a short time for problems of sizes up to 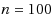$n=100$ . The MIP model finds guaranteed optimum partitions efficiently for sizes up to 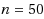$n=50$ . The number partitioning problem (NPP) is to divide 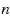$n$ numbers 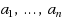$a_1,\dots ,a_n$ into two disjoint subsets such that the difference between the two subset sums – the discrepancy, 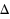$\Delta$ , is minimized. In the balanced version of the NPP (BalNPP), the subsets must have the same cardinality. With the 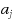$a_j$ chosen uniformly from 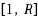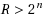$[1,R]$ , $R>2^n$ gives the hard phase, when there are no equal partitions (i.e., 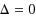$\Delta =0$ ) with high probability (whp). In this phase, the minimum partition is also unique whp. Most current methods struggle in the hard phase, as they often perform exhaustive enumeration of all partitions to find the optimum.