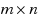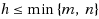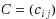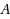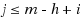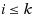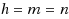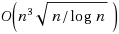| Article ID: | iaor20124606 |
| Volume: | 9 |
| Issue: | 3 |
| Start Page Number: | 149 |
| End Page Number: | 158 |
| Publication Date: | Aug 2012 |
| Journal: | Discrete Optimization |
| Authors: | Romero David, Calvillo Gilberto |
| Keywords: | matrices, sets |
We prove the following remarkable fact for matrices with entries from an ordered set: For any