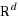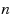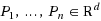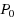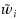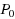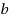| Article ID: | iaor20124602 |
| Volume: | 9 |
| Issue: | 3 |
| Start Page Number: | 137 |
| End Page Number: | 148 |
| Publication Date: | Aug 2012 |
| Journal: | Discrete Optimization |
| Authors: | Hatzl Johannes |
| Keywords: | combinatorial optimization, location |
In this paper, we consider the 1‐median problem in