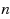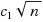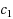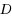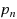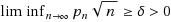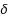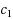The best choice problem for upward directed graphs

We consider a generalization of the best choice problem to upward directed graphs. We describe a strategy for choosing a maximal element (i.e., an element with no outgoing edges) when a selector knows in advance only the number $n$ of vertices of the graph. We show that, as long as the number of elements dominated directly by the maximal ones is not greater than $c_1\sqrt{n}$ for some positive constant $c_1$ and the indegree of remaining vertices is bounded by a constant $D$ , the probability $p_n$ of the right choice according to our strategy satisfies ${lim\; inf}_{n\to \infty }{p}_n\sqrt{n}\ge \delta >0$ , where $\delta$ is a constant depending on $c_1$ and $D$ .