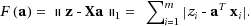We consider the problem of searching for a best LAD‐solution of an overdetermined system of linear equations Xa=z, X∈ ℝ
m×n
, m≥n,
 . This problem is equivalent to the problem of determining a best LAD‐hyperplane x↦a
T
x, x∈ ℝ
n
on the basis of given data
. This problem is equivalent to the problem of determining a best LAD‐hyperplane x↦a
T
x, x∈ ℝ
n
on the basis of given data
 , whereby the minimizing functional is of the form
, whereby the minimizing functional is of the form
 An iterative procedure is constructed as a sequence of weighted median problems, which gives the solution in finitely many steps. A criterion of optimality follows from the fact that the minimizing functional F is convex, and therefore the point a
*∈ ℝ
n
is the point of a global minimum of the functional F if and only if 0∈∂F(a
*). Motivation for the construction of the algorithm was found in a geometrically visible algorithm for determining a best LAD‐plane (x,y)↦αx+βy, passing through the origin of the coordinate system, on the basis of the data (x
i
,y
i
,z
i
),i=1,…,m.
An iterative procedure is constructed as a sequence of weighted median problems, which gives the solution in finitely many steps. A criterion of optimality follows from the fact that the minimizing functional F is convex, and therefore the point a
*∈ ℝ
n
is the point of a global minimum of the functional F if and only if 0∈∂F(a
*). Motivation for the construction of the algorithm was found in a geometrically visible algorithm for determining a best LAD‐plane (x,y)↦αx+βy, passing through the origin of the coordinate system, on the basis of the data (x
i
,y
i
,z
i
),i=1,…,m.