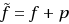| Article ID: | iaor20112655 |
| Volume: | 149 |
| Issue: | 1 |
| Start Page Number: | 1 |
| End Page Number: | 25 |
| Publication Date: | Apr 2011 |
| Journal: | Journal of Optimization Theory and Applications |
| Authors: | An T, Phu X, Pho M |
| Keywords: | programming: quadratic, programming: convex |
The problem of maximizing