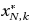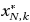In this paper, we study the link between a Chance‐Constrained optimization Problem (CCP) and its sample counterpart (SP). SP has a finite number, say N, of sampled constraints. Further, some of these sampled constraints, say k, are discarded, and the final solution is indicated by
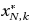. Extending previous results on the feasibility of sample convex optimization programs, we establish the feasibility of
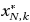for the initial CCP problem. Constraints removal allows one to improve the cost function at the price of a decreased feasibility. The cost improvement can be inspected directly from the optimization result, while the theory here developed permits to keep control on the other side of the coin, the feasibility of the obtained solution. In this way, trading feasibility for performance is put on solid mathematical grounds in this paper. The feasibility result here obtained applies to a vast class of chance‐constrained optimization problems, and has the distinctive feature that it holds true irrespective of the algorithm used to discard k constraints in the SP problem. For constraints discarding, one can thus, e.g., resort to one of the many methods introduced in the literature to solve chance‐constrained problems with discrete distribution, or even use a greedy algorithm, which is computationally very low‐demanding, and the feasibility result remains intact. We further prove that, if constraints in the SP problem are optimally removed–i.e., one deletes those constraints leading to the largest possible cost improvement–, then a precise optimality link to the original chance‐constrained problem CCP in addition holds.
