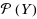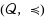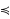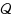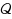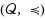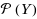New Order Relations in Set Optimization

In this paper we study a set optimization problem (SOP), i.e. we minimize a set‐valued objective map F, which takes values on a real linear space Y equipped with a pre‐order induced by a convex cone K. We introduce new order relations on the power set 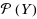$𝒫(Y)$ of Y (or on a subset of it), which are more suitable from a practical point of view than the often used minimizers in set optimization. Next, we propose a simple two‐steps unifying approach to studying (SOP) w.r.t. various order relations. Firstly, we extend in a unified scheme some basic concepts of vector optimization, which are defined on the space Y up to an arbitrary nonempty pre‐ordered set 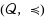$(𝒬,\preccurlyeq )$ without any topological or linear structure. Namely, we define the following concepts w.r.t. the pre‐order 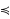$\preccurlyeq$ : minimal elements, semicompactness, completeness, domination property of a subset of 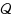$𝒬$ , and semicontinuity of a set‐valued map with values in 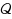$𝒬$ in a topological setting. Secondly, we establish existence results for optimal solutions of (SOP), when F takes values on 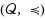$(𝒬,\preccurlyeq )$ from which one can easily derive similar results for the case, when F takes values on 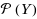$𝒫(Y)$ equipped with various order relations.