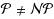Absolute approximation ratios for packing rectangles into bins

We consider the problem of packing rectangles into bins that are unit squares, where the goal is to minimize the number of bins used. All rectangles have to be packed non‐overlapping and orthogonal, i.e., axis‐parallel. We present an algorithm with an absolute worst‐case ratio of 2 for the case where the rectangles can be rotated by 90 degrees. This is optimal provided $𝒫\ne \mathrm{𝒩𝒫}$ . For the case where rotation is not allowed, we prove an approximation ratio of 3 for the algorithm Hybrid First Fit which was introduced by Chung et al. (SIAM J. Algebr. Discrete Methods 3(1):66–76, 1982) and whose running time is slightly better than the running time of Zhang’s previously known 3‐approximation algorithm (Zhang in Oper. Res. Lett. 33(2):121–126, 2005).