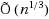Fully Dynamic Geometric Spanners

In this paper we present an algorithm for maintaining a spanner over a dynamic set of points in constant doubling dimension metric spaces. For a set S of points in ℝ ^d , a t‐spanner is a sparse graph on the points of S such that there is a path in the spanner between any pair of points whose total length is at most t times the distance between the points. We present the first fully dynamic algorithm for maintaining a spanner whose update time depends solely on the number of points in S. In particular, we show how to maintain a (1+ϵ)‐spanner with O(n/ϵ ^d ) edges, where points can be inserted to S in an amortized update time of O(log n) and deleted from S in an amortized update time of 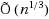$Õ(n^{1/3})$ . As a by‐product of our techniques we obtain a simple incremental algorithm for constructing a (1+ϵ)‐spanner with O(n/ϵ ^d ) edges in constant doubling dimension metric spaces whose running time is O(nlog n).