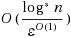We consider the problem of partitioning the set of vertices of a given unit disk graph (UDG) into a minimum number of cliques. The problem is NP‐hard and various constant factor approximations are known, with the current best ratio of 3. Our main result is a weakly robust polynomial time approximation scheme (PTAS) for UDGs expressed with edge‐lengths that either (i) computes a clique partition or (ii) gives a certificate that the graph is not a UDG; for the case (i) it computes a clique partition having size that is guaranteed to be within (1+ϵ) of the optimum size if the input is UDG; however if the input is not a UDG it either computes a clique partition as in case (i) with no guarantee on the quality of the clique partition or detects that it is not a UDG. Noting that recognition of UDG’s is NP‐hard even if we are given edge lengths, our PTAS is a weakly‐robust algorithm. Our algorithm can be transformed into an
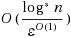time distributed PTAS. We consider a weighted version of the clique partition problem on vertex‐weighted UDGs that generalizes the problem. We note some key distinctions with the unweighted version, where ideas useful in obtaining a PTAS break down. Yet, surprisingly, it admits a (2+ϵ)‐approximation algorithm for the weighted case where the graph is expressed, say, as an adjacency matrix. This improves on the best known 8‐approximation for the unweighted case for UDGs expressed in standard form.
