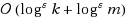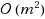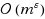| Article ID: | iaor2012409 |
| Volume: | 62 |
| Issue: | 3 |
| Start Page Number: | 733 |
| End Page Number: | 753 |
| Publication Date: | Apr 2012 |
| Journal: | Algorithmica |
| Authors: | Hoefer Martin, Briest Patrick, Krysta Piotr |
| Keywords: | optimization |
We study a multi‐player one‐round game termed Stackelberg Network Pricing Game, in which a