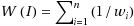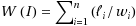Windows scheduling of arbitrary‐length jobs on multiple machines

The generalized windows scheduling problem for n jobs on multiple machines is defined as follows: Given is a sequence, I=⟨(w 1,𝓁 1),(w 2,𝓁 2),…,(w n ,𝓁 n )⟩ of n pairs of positive integers that are associated with the jobs 1,2,…,n, respectively. The processing length of job i is 𝓁 i slots where a slot is the processing time of one unit of length. The goal is to repeatedly and non‐preemptively schedule all the jobs on the fewest possible machines such that the gap (window) between two consecutive beginnings of executions of job i is at most w i slots. This problem arises in push broadcast systems in which data are transmitted on multiple channels. The problem is NP‐hard even for unit‐length jobs and a (1+ϵ)‐approximation algorithm is known for this case by approximating the natural lower bound 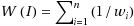$W(I)={\sum }_{i=1}^n(1/w_i)$ . The techniques used for approximating unit‐length jobs cannot be extended for arbitrary‐length jobs mainly because the optimal number of machines might be arbitrarily larger than the generalized lower bound 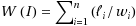$W(I)={\sum }_{i=1}^n({\ell }_i/w_i)$ . The main result of this paper is an 8‐approximation algorithm for the WS problem with arbitrary lengths using new methods, different from those used for the unit‐length case. The paper also presents another algorithm that uses 2(1+ϵ)W(I)+logw max machines and a greedy algorithm that is based on a new tree representation of schedules. The greedy algorithm is optimal for some special cases, and computational experiments show that it performs very well in practice.