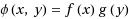Convex envelopes of products of convex and component‐wise concave functions

In this paper, we consider functions of the form 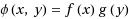$\varphi (x,y)=f(x)g(y)$ over a box, where f(x)x∈ℝ is a nonnegative monotone convex function with a power or an exponential form, and g(y)y∈ℝⁿ is a component‐wise concave function which changes sign over the vertices of its domain. We derive closed‐form expressions for convex envelopes of various functions in this category. We demonstrate via numerical examples that the proposed envelopes are significantly tighter than popular factorable programming relaxations.