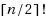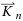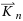TSP Heuristics: Domination Analysis and Complexity

We show that the 2‐Opt and 3‐Opt heuristics for the traveling salesman problem (TSP) on the complete graph Kn produce a solution no worse than the average cost of a tour in Kn in a polynomial number of iterations. As a consequence, we get that the domination numbers of the 2‐ Opt , 3‐ Opt , Carlier–Villon, Shortest Path Ejection Chain, and Lin–Kernighan heuristics are all at least (n‐2)! / 2 . The domination number of the Christofides heuristic is shown to be no more than $\lceil n/2\mathrm{ceil}!$ , and for the Double Tree heuristic and a variation of the Christofides heuristic the domination numbers are shown to be one (even if the edge costs satisfy the triangle inequality). Further, unless P = NP, no polynomial time approximation algorithm exists for the TSP on the complete digraph ${\stackrel{\rightharpoonup }{K}}_n$ with domination number at least (n‐1)!‐k for any constant k or with domination number at least (n‐1)! ‐ (( k /(k+1))(n+r))!‐1 for any non‐negative constants r and k such that (n+r) $\equiv$ 0 mod (k+1). The complexities of finding the median value of costs of all the tours in ${\stackrel{\rightharpoonup }{K}}_n$ and of similar problems are also studied.