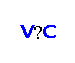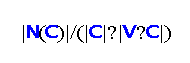Cliques with maximum/minimum edge neighborhood and neighborhood density

This paper addresses maximum/minimum edge neighborhood and neighborhood density cliques in G. Two versions will be undertaken, by fixing, or not, the size of the cliques. From an optimization point of view these problems do not bring much novelty, as they can be seen as particular or special versions of weighted clique problems. However, from a practical point of view, they concentrate on certain kinds of properties of cliques, rather than their size, revealing clique's engagement in the graph. In fact, a maximum edge neighborhood clique should be strongly embraced in the graph, while a minimum edge neighborhood clique should reveal an almost isolated strong component. In particular, special versions of the new problems allow to distinguish among cliques of the same size, namely among possible tied maximum cliques in the graph. We propose node based formulations for these edge based clique related problems. Using these models, we present computational results and suggest applications where the new problems can bring additional insights. Given a graph G=(V,E) and a clique C of G, the edge neighborhood of C can be defined as the total number of edges running between C and 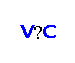$V?C$ , being denoted by N(C). 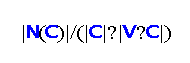The density of the edge neighborhood N(C) can be set as the ratio ( $|N(C)|/(|C|?|V?C|)$ ).