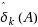Computing the Maximum Degree of Minors in Matrix Pencils via Combinatorial Relaxation

This paper presents a new algorithm for computing the maximum degree δk (A) of a minor of order k in a matrix pencil A(s) . The problem is of practical significance in the field of numerical analysis and systems control. The algorithm adopts a general framework of “combinatorial relaxation” due to Murota. It first solves the weighted bipartite matching problem to obtain an estimate ${\hat{\delta }}_k(A)$ on δk (A) , and then checks if the estimate is correct, exploiting the optimal dual solution. In case of incorrectness, it modifies the matrix pencil A(s) to improve the estimate ${\hat{\delta }}_k(A)$ without changing δk(A) .The present algorithm performs this matrix modification by an equivalence transformation with constant matrices, whereas the previous one uses biproper rational function matrices. Thus the present approach saves memory space and reduces the running time bound by a factor of rank A.