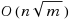Faster Swap Edge Computation in Minimum Diameter Spanning Trees

In network communication systems, frequently messages are routed along a minimum diameter spanning tree (MDST) of the network, to minimize the maximum travel time of messages. When a transient failure disables an edge of the MDST, the network is disconnected, and a temporary replacement edge must be chosen, which should ideally minimize the diameter of the new spanning tree. Such a replacement edge is called a best swap. Preparing for the failure of any edge of the MDST, the all‐best‐swaps (ABS) problem asks for finding the best swap for every edge of the MDST. Given a 2‐edge‐connected weighted graph G=(V,E), where |V|=n and |E|=m, we solve the ABS problem in O(mlog n) time and O(m) space, thus considerably improving upon the decade‐old previously best solution, which requires 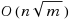$O(n\sqrt{m})$ time and O(m) space, for m=o(n ²/log ² n).