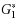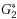Exact and approximation algorithms for the complementary maximal strip recovery problem

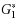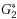Given two genomic maps G 1 and G 2 each represented as a sequence of n gene markers, the maximal strip recovery (MSR) problem is to retain the maximum number of markers in both G 1 and G 2 such that the resultant subsequences, denoted as $G_1^{*}$ and $G_2^{*}$ , can be partitioned into the same set of maximal substrings of length greater than or equal to two. Such substrings can occur in the reversal and negated form. The complementary maximal strip recovery (CMSR) problem is to delete the minimum number of markers from both G 1 and G 2 for the same purpose, with its optimization goal exactly complementary to maximizing the total number of gene markers retained in the final maximal substrings. Both MSR and CMSR have been shown NP‐hard and APX‐hard. A 4‐approximation algorithm is known for the MSR problem, but no constant ratio approximation algorithm for CMSR. In this paper, we present an O(3 ^k n ²)‐time fixed‐parameter tractable (FPT) algorithm, where k is the size of the optimal solution, and a 3‐approximation algorithm for the CMSR problem.