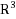The Molecular Distance Geometry Problem (MDGP) consists in finding an embedding in
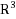of a nonnegatively weighted simple undirected graph with the property that the Euclidean distances between embedded adjacent vertices must be the same as the corresponding edge weights. The Discretizable Molecular Distance Geometry Problem (DMDGP) is a particular subset of the MDGP which can be solved using a discrete search occurring in continuous space; its main application is to find three‐dimensional arrangements of proteins using Nuclear Magnetic Resonance (NMR) data. The model provided by the DMDGP, however, is too abstract to be directly applicable in proteomics. In the last five years our efforts have been directed towards adapting the DMDGP to be an ever closer model of the actual difficulties posed by the problem of determining protein structures from NMR data. This survey lists recent developments on DMDGP related research.
