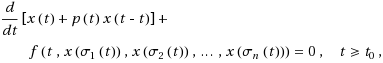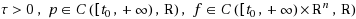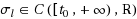This paper deals with the first order nonlinear neutral delay differential equation
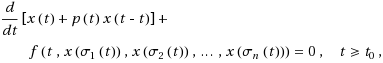 where
where
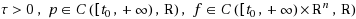 and
and
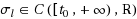 with lim
t→+∞
σ
l
(t)=+∞ for l ∈{1, 2, … ,
n}. By using the Banach fixed point theorem, we prove the global existence of uncountably many bounded positive solutions for the above equation relative to all ranges of the function p, construct some Mann type iterative algorithms with errors to approximate these positive solutions and discuss several error estimates between the sequences generated by the iterative algorithms and these positive solutions. Seven examples are presented to illuminate the results obtained in this paper.
with lim
t→+∞
σ
l
(t)=+∞ for l ∈{1, 2, … ,
n}. By using the Banach fixed point theorem, we prove the global existence of uncountably many bounded positive solutions for the above equation relative to all ranges of the function p, construct some Mann type iterative algorithms with errors to approximate these positive solutions and discuss several error estimates between the sequences generated by the iterative algorithms and these positive solutions. Seven examples are presented to illuminate the results obtained in this paper.