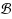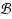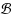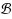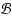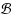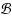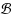Let
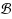 be a centrally symmetric convex polygon of ℝ2 and ∥p-q∥ be the distance between two points p,q∈ ℝ2 in the normed plane whose unit ball is
be a centrally symmetric convex polygon of ℝ2 and ∥p-q∥ be the distance between two points p,q∈ ℝ2 in the normed plane whose unit ball is
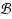 . For a set T of n points (terminals) in ℝ2, a
. For a set T of n points (terminals) in ℝ2, a
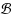 ‐network on T is a network N(T)=(V,E) with the property that its edges are parallel to the directions of
‐network on T is a network N(T)=(V,E) with the property that its edges are parallel to the directions of
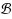 and for every pair of terminals t
i
and t
j
, the network N(T) contains a shortest
and for every pair of terminals t
i
and t
j
, the network N(T) contains a shortest
 ‐path between them, i.e., a path of length ∥t
i
-t
j
∥. A minimum
‐path between them, i.e., a path of length ∥t
i
-t
j
∥. A minimum
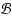 ‐network on T is a
‐network on T is a
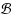 ‐network of minimum possible length. The problem of finding minimum
‐network of minimum possible length. The problem of finding minimum
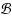 ‐networks has been introduced by Gudmundsson, Levcopoulos, and Narasimhan (APPROX’99) in the case when the unit ball
‐networks has been introduced by Gudmundsson, Levcopoulos, and Narasimhan (APPROX’99) in the case when the unit ball
 is a square (and hence the distance ∥p-q∥ is the l
1 or the l
∞‐distance between p and q) and it has been shown recently by Chin, Guo, and Sun (Symposium on Computational Geometry, pp. 393–402, 2009) to be strongly NP‐complete. Several approximation algorithms (with factors 8, 4, 3, and 2) for the minimum Manhattan problem are known. In this paper, we propose a factor 2.5 approximation algorithm for the minimum
is a square (and hence the distance ∥p-q∥ is the l
1 or the l
∞‐distance between p and q) and it has been shown recently by Chin, Guo, and Sun (Symposium on Computational Geometry, pp. 393–402, 2009) to be strongly NP‐complete. Several approximation algorithms (with factors 8, 4, 3, and 2) for the minimum Manhattan problem are known. In this paper, we propose a factor 2.5 approximation algorithm for the minimum
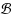 ‐network problem. The algorithm employs a simplified version of the strip‐staircase decomposition proposed in our paper (Chepoi et al. in Theor. Comput. Sci. 390:56–69, 2008, and APPROX‐RANDOM, pp. 40–51, 2005) and subsequently used in other factor 2 approximation algorithms for the minimum Manhattan problem.
‐network problem. The algorithm employs a simplified version of the strip‐staircase decomposition proposed in our paper (Chepoi et al. in Theor. Comput. Sci. 390:56–69, 2008, and APPROX‐RANDOM, pp. 40–51, 2005) and subsequently used in other factor 2 approximation algorithms for the minimum Manhattan problem.