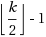We study the problem of packing element‐disjoint Steiner trees in graphs. We are given a graph and a designated subset of terminal nodes, and the goal is to find a maximum cardinality set of element‐disjoint trees such that each tree contains every terminal node. An element means a non‐terminal node or an edge. (Thus, each non‐terminal node and each edge must be in at most one of the trees.) We show that the problem is APX‐hard when there are only three terminal nodes, thus answering an open question. Our main focus is on the special case when the graph is planar. We show that the problem of finding two element‐disjoint Steiner trees in a planar graph is NP‐hard. Similarly, the problem of finding two edge‐disjoint Steiner trees in a planar graph is NP‐hard. We design an algorithm for planar graphs that achieves an approximation guarantee close to 2. In fact, given a planar graph that is k element‐connected on the terminals (k is an upper bound on the number of element‐disjoint Steiner trees), the algorithm returns
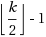 element‐disjoint Steiner trees. Using this algorithm, we get an approximation algorithm for the edge‐disjoint version of the problem on planar graphs that improves on the previous approximation guarantees. We also show that the natural LP relaxation of the planar problem has an integrality ratio approaching 2.
element‐disjoint Steiner trees. Using this algorithm, we get an approximation algorithm for the edge‐disjoint version of the problem on planar graphs that improves on the previous approximation guarantees. We also show that the natural LP relaxation of the planar problem has an integrality ratio approaching 2.