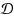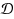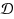We consider the (undirected) Node Connectivity Augmentation (NCA) problem: given a graph J=(V,E
J
) and connectivity requirements
 , find a minimum size set I of new edges (any edge is allowed) such that the graph J∪I contains r(u,v) internally‐disjoint uv‐paths, for all u,v∈V. In Rooted NCA there is s∈V such that r(u,v)>0 implies u=s or v=s. For large values of k=max
u,v∈V
r(u,v), NCA is at least as hard to approximate as Label‐Cover and thus it is unlikely to admit an approximation ratio polylogarithmic in k. Rooted NCA is at least as hard to approximate as Hitting‐Set. The previously best approximation ratios for the problem were O(kln n) for NCA and O(ln n) for Rooted NCA. In this paper we give an approximation algorithm with ratios O(kln 2
k) for NCA and O(ln 2
k) for Rooted NCA. This is the first approximation algorithm with ratio independent of n, and thus is a constant for any fixed k. Our algorithm is based on the following new structural result which is of independent interest. If
, find a minimum size set I of new edges (any edge is allowed) such that the graph J∪I contains r(u,v) internally‐disjoint uv‐paths, for all u,v∈V. In Rooted NCA there is s∈V such that r(u,v)>0 implies u=s or v=s. For large values of k=max
u,v∈V
r(u,v), NCA is at least as hard to approximate as Label‐Cover and thus it is unlikely to admit an approximation ratio polylogarithmic in k. Rooted NCA is at least as hard to approximate as Hitting‐Set. The previously best approximation ratios for the problem were O(kln n) for NCA and O(ln n) for Rooted NCA. In this paper we give an approximation algorithm with ratios O(kln 2
k) for NCA and O(ln 2
k) for Rooted NCA. This is the first approximation algorithm with ratio independent of n, and thus is a constant for any fixed k. Our algorithm is based on the following new structural result which is of independent interest. If
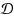 is a set of node pairs in a graph J, then the maximum degree in the hypergraph formed by the inclusion minimal tight sets separating at least one pair in
is a set of node pairs in a graph J, then the maximum degree in the hypergraph formed by the inclusion minimal tight sets separating at least one pair in
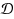 is O(𝓁
2), where 𝓁 is the maximum connectivity in J of a pair in
is O(𝓁
2), where 𝓁 is the maximum connectivity in J of a pair in
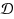 .
.