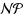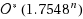The Power Dominating Set problem is an extension of the well‐known domination problem on graphs in a way that we enrich it by a second propagation rule: given a graph G(V,E), a set P⊆V is a power dominating set if every vertex is observed after the exhaustive application of the following two rules. First, a vertex is observed if v∈P or it has a neighbor in P. Secondly, if an observed vertex has exactly one unobserved neighbor u, then also u will be observed, as well. We show that Power Dominating Set remains
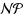‐hard on cubic graphs. We design an algorithm solving this problem in time
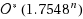on general graphs, using polynomial space only. To achieve this, we introduce so‐called reference search trees that can be seen as a compact representation of usual search trees, providing non‐local pointers in order to indicate pruned subtrees.
