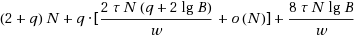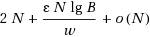We present two results for path traversal in trees, where the traversal is performed in an asymptotically optimal number of I/Os and the tree structure is represented succinctly. Our first result is for bottom‐up traversal that starts with a node in a tree on N nodes and traverses a path to the root. We show how a tree T on N nodes with q‐bit keys, where q=O(lg N), can be blocked in a succinct fashion such that a bottom‐up traversal requires O(K/B+1) I/Os using only
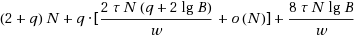 bits to store T for any constant 0<τ
<1, where K is the path length and w is the word size. This data structure is succinct because the above space cost is at most (2+q)N+q·(ηN+o(N)) bits for any arbitrarily selected constant, η, such that 0<η
<1. When storing keys with tree nodes is not required, we can represent T in
bits to store T for any constant 0<τ
<1, where K is the path length and w is the word size. This data structure is succinct because the above space cost is at most (2+q)N+q·(ηN+o(N)) bits for any arbitrarily selected constant, η, such that 0<η
<1. When storing keys with tree nodes is not required, we can represent T in
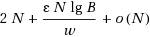 bits, where ϵ is an arbitrarily selected constant such that 0<ϵ
<1, while providing the same support for queries. Our second result is for top‐down traversal in binary trees. We store the tree in (3+q)N+o(N) bits, while top‐down traversal can still be performed in an asymptotically optimal number of I/Os.
bits, where ϵ is an arbitrarily selected constant such that 0<ϵ
<1, while providing the same support for queries. Our second result is for top‐down traversal in binary trees. We store the tree in (3+q)N+o(N) bits, while top‐down traversal can still be performed in an asymptotically optimal number of I/Os.