We consider a general framework in which a memoryless robot periodically explores all the nodes of a connected anonymous graph by following local information available at each vertex. For each vertex v, the endpoints of all edges adjacent to v are assigned unique labels within the range 1 to deg (v) (the degree of v). The generic exploration strategy is implemented using a right‐hand‐rule transition function: after entering vertex v via the edge labeled i, the robot proceeds with its exploration, leaving via the edge having label [i mod deg (v)]+1 at v. A lot of attention has been given to the problem of labeling the graph so as to achieve a periodic exploration having the minimum possible length π. It has recently been proved (Czyzowicz et al., 2009) that
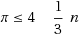holds for all graphs of n vertices. Herein, we provide a new labeling scheme which leads to shorter exploration cycles, improving the general bound to π≤4n-2. This main result is shown to be tight with respect to the class of labellings admitting certain connectivity properties. The labeling scheme is based on a new graph decomposition which may be of independent interest.
