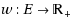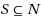Computing solutions for matching games

A matching game is a cooperative game (N, v) defined on a graph G = (N, E) with an edge weighting 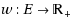$$w:E\to {ℝ}_{+}$$ . The player set is N and the value of a coalition 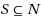$S\subseteq N$ is defined as the maximum weight of a matching in the subgraph induced by S. First we present an O(nm + n ² log n) algorithm that tests if the core of a matching game defined on a weighted graph with n vertices and m edges is nonempty and that computes a core member if the core is nonempty. This algorithm improves previous work based on the ellipsoid method and can also be used to compute stable solutions for instances of the stable roommates problem with payments. Second we show that the nucleolus of an n‐player matching game with a nonempty core can be computed in O(n ⁴) time. This generalizes the corresponding result of Solymosi and Raghavan for assignment games. Third we prove that is NP‐hard to determine an imputation with minimum number of blocking pairs, even for matching games with unit edge weights, whereas the problem of determining an imputation with minimum total blocking value is shown to be polynomial‐time solvable for general matching games.