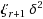On duality gap in binary quadratic programming

We investigate in this paper the duality gap between the binary quadratic optimization problem and its semidefinite programming relaxation. We show that the duality gap can be underestimated by ${\xi }_{r+1}{\delta }^2$ , where δ is the distance between {-1, 1} ⁿ and certain affine subspace, and ξ r+1 is the smallest positive eigenvalue of a perturbed matrix. We also establish the connection between the computation of δ and the cell enumeration of hyperplane arrangement in discrete geometry.