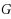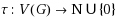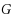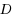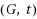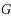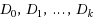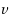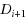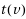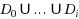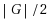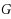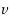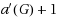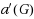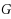Let
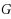 be a graph and
be a graph and
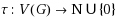 be an assignment of thresholds to the vertices of
be an assignment of thresholds to the vertices of
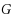 . A subset of vertices
. A subset of vertices
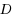 is said to be a dynamic monopoly corresponding to
is said to be a dynamic monopoly corresponding to
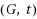 if the vertices of
if the vertices of
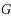 can be partitioned into subsets
can be partitioned into subsets
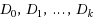 such that
such that
 and for any
and for any
 , each vertex
, each vertex
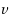 in
in
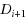 has at least
has at least
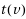 neighbors in
neighbors in
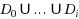 . Dynamic monopolies are in fact modeling the irreversible spread of influence in social networks. In this paper we first obtain a lower bound for the smallest size of any dynamic monopoly in terms of the average threshold and the order of graph. Also we obtain an upper bound in terms of the minimum vertex cover of graphs. Then we derive the upper bound
. Dynamic monopolies are in fact modeling the irreversible spread of influence in social networks. In this paper we first obtain a lower bound for the smallest size of any dynamic monopoly in terms of the average threshold and the order of graph. Also we obtain an upper bound in terms of the minimum vertex cover of graphs. Then we derive the upper bound
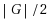 for the smallest size of any dynamic monopoly when the graph
for the smallest size of any dynamic monopoly when the graph
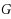 contains at least one odd vertex, where the threshold of any vertex
contains at least one odd vertex, where the threshold of any vertex
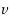 is set as
is set as
 (i.e. strict majority threshold). This bound improves the best known bound for strict majority threshold. We show that the latter bound can be achieved by a polynomial time algorithm. We also show that
(i.e. strict majority threshold). This bound improves the best known bound for strict majority threshold. We show that the latter bound can be achieved by a polynomial time algorithm. We also show that
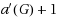 is an upper bound for the size of strict majority dynamic monopoly, where
is an upper bound for the size of strict majority dynamic monopoly, where
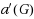 stands for the matching number of
stands for the matching number of
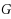 . Finally, we obtain a basic upper bound for the smallest size of any dynamic monopoly, in terms of the average threshold and vertex degrees. Using this bound we derive some other upper bounds.
. Finally, we obtain a basic upper bound for the smallest size of any dynamic monopoly, in terms of the average threshold and vertex degrees. Using this bound we derive some other upper bounds.