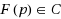| Article ID: | iaor20123826 |
| Volume: | 53 |
| Issue: | 1 |
| Start Page Number: | 5 |
| End Page Number: | 28 |
| Publication Date: | May 2012 |
| Journal: | Journal of Global Optimization |
| Authors: | Yao Jen-Chih, Wang Jin-Hua, Li Chong |
| Keywords: | Newton method |
A notion of quasi‐regularity is extended for the inclusion problem