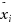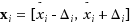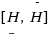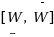Most applications of statistics to science and engineering are based on the assumption that the corresponding random variables are normally distributed, i.e., distributed according to Gaussian law in which the probability density function ρ(x) exponentially decreases with x: ρ(x)∼exp(-k·x
2). Normal distributions indeed frequently occur in practice. However, there are also many practical situations, including situations from mathematical finance, in which we encounter heavy‐tailed distributions, i.e., distributions in which ρ(x) decreases as ρ(x)∼x
-α
. To properly take this uncertainty into account when making decisions, it is necessary to estimate the parameters of such distributions based on the sample data x
1,…,x
n
–and thus, to predict the size and the probabilities of large deviations. The most well‐known statistical estimates for such distributions are the Hill estimator H for α and the Weismann estimator W for the corresponding quantiles. These estimators are based on the simplifying assumption that the sample values x
i
are known exactly. In practice, we often know the values x
i
only approximately–e.g., we know the estimates
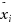 and we know the upper bounds ?
i
on the estimation errors. In this case, the only information that we have about the actual (unknown) value x
i
is that x
i
belongs to the interval
and we know the upper bounds ?
i
on the estimation errors. In this case, the only information that we have about the actual (unknown) value x
i
is that x
i
belongs to the interval
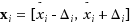 . Different combinations of values x
i
∈x
i
lead, in general, to different values of H and W. It is therefore desirable to find the ranges
. Different combinations of values x
i
∈x
i
lead, in general, to different values of H and W. It is therefore desirable to find the ranges
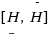 and
and
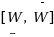 of possible values of H and W. In this paper, we describe efficient algorithms for computing these ranges.
of possible values of H and W. In this paper, we describe efficient algorithms for computing these ranges.