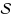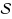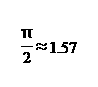Minimum‐Perimeter Intersecting Polygons

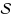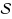Given a set $𝒮$ of segments in the plane, a polygon P is an intersecting polygon of $𝒮$ if every segment in $𝒮$ intersects the interior or the boundary of P. The problem MPIP of computing a minimum‐perimeter intersecting polygon of a given set of n segments in the plane was first considered by Rappaport in 1995. This problem is not known to be polynomial, nor it is known to be NP‐hard. Rappaport (Int. J. Comput. Geom. Appl. 5:243–265, 1995) gave an exponential‐time exact algorithm for MPIP. Hassanzadeh and Rappaport (Proceedings of the 23rd International Workshop on Algorithms and Data Structures, LNCS, vol. 5664, pp. 363–374, 2009) gave a polynomial‐time approximation algorithm with ratio 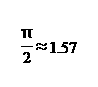$\frac{\pi }{2}\approx 1.57$ . In this paper, we present two improved approximation algorithms for MPIP: a 1.28‐approximation algorithm by linear programming, and a polynomial‐time approximation scheme by discretization and enumeration. Our algorithms can be generalized for computing an approximate minimum‐perimeter intersecting polygon of a set of convex polygons in the plane. From the other direction, we show that computing a minimum‐perimeter intersecting polygon of a set of (not necessarily convex) simple polygons is NP‐hard.