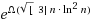Pairs of Complementary Unary Languages with ‘Balanced’ Nondeterministic Automata

For each sufficiently large n, there exists a unary regular language L such that both L and its complement L ^c are accepted by unambiguous nondeterministic automata with at most n states, while the smallest deterministic automata for these two languages still require a superpolynomial number of states, at least 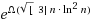$e^{\Omega (\sqrt{[}3]n\cdot {\ln }^{2}n)}$ . Actually, L and L ^c are ‘balanced’ not only in the number of states but, moreover, they are accepted by nondeterministic machines sharing the same transition graph, differing only in the distribution of their final states. As a consequence, the gap between the sizes of unary unambiguous self‐verifying automata and deterministic automata is also superpolynomial.