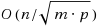We consider a simple restriction of the PRAM model (called PPRAM), where the input is arbitrarily partitioned between a fixed set of p processors and the shared memory is restricted to m cells. This model allows for investigation of the tradeoffs/ bottlenecks with respect to the communication bandwidth (modeled by the shared memory size m ) and the number of processors p . The model is quite simple and allows the design of optimal algorithms without losing the effect of communication bottlenecks. We have focused on the PPRAM complexity of problems that have Õ (n) sequential solutions (where n is the input size), and where m ≤ p ≤ n . We show essentially tight time bounds (up to logarithmic factors) for several problems in this model such as summing, Boolean threshold, routing, integer sorting, list reversal and k ‐selection. We get typically two sorts of complexity behaviors for these problems: One type is Õ (n/p + p/m) , which means that the time scales with the number of processors and with memory size (in appropriate ranges) but not with both. The other is Õ (n/m) , which means that the running time does not scale with p and reflects a communication bottleneck (as long as m < p ). We are not aware of any problem whose complexity scales with both p and m (e.g.
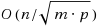). This might explain why in actual implementations one often fails to get p ‐scalability for p close to n .
