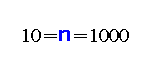Minimizing total weighted flow time under uncertainty using dominance and a stability box

We consider an uncertain single‐machine scheduling problem, in which the processing time of a job can take any real value on a given closed interval. The criterion is to minimize the total weighted flow time of the n jobs, where there is a weight associated with a job. We calculate a number of minimal dominant sets of the job permutations (a minimal dominant set contains at least one optimal permutation for each possible scenario). We introduce a new stability measure of a job permutation (a stability box) and derive an exact formula for the stability box, which runs in O(n log n) time. We investigate properties of a stability box. These properties allow us to develop an O(n ²)‐algorithm for constructing a permutation with the largest volume of a stability box. If several permutations have the largest volume of a stability box, the developed algorithm selects one of them due to a simple heuristic. 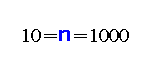The efficiency of the constructed permutation is demonstrated on a large set of randomly generated instances with $10=n=1000$ .