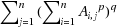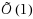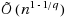We consider the problem of estimating hybrid frequency moments of two dimensional data streams. In this model, data is viewed to be organized in a matrix form (A
i,j
)1≤i,j,≤n
. The entries A
i,j
are updated coordinate‐wise, in arbitrary order and possibly multiple times. The updates include both increments and decrements to the current value of A
i,j
. The hybrid frequency moment F
p,q
(A) is defined as
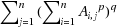 and is a generalization of the frequency moment of one‐dimensional data streams. We present the first
and is a generalization of the frequency moment of one‐dimensional data streams. We present the first
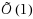 space algorithm for the problem of estimating F
p,q
for p∈[0,2] and q∈[0,1] to within an approximation factor of 1±ϵ. The
space algorithm for the problem of estimating F
p,q
for p∈[0,2] and q∈[0,1] to within an approximation factor of 1±ϵ. The
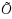 notation hides poly‐logarithmic factors in the size of the stream m, the matrix size n and polynomial factors of ϵ
-1. We also present the first
notation hides poly‐logarithmic factors in the size of the stream m, the matrix size n and polynomial factors of ϵ
-1. We also present the first
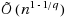 space algorithm for estimating F
p,q
for p∈[0,2] and q?(1,2].
space algorithm for estimating F
p,q
for p∈[0,2] and q?(1,2].