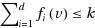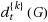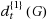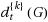For a positive integer k, a total {k}‐dominating function of a graph G is a function f from the vertex set V(G) to the set {0,1,2,…,k} such that for any vertex v∈V(G), the condition Σ
u∈N(v)
f(u)≥k is fulfilled, where N(v) is the open neighborhood of v. A set {f
1,f
2,…,f
d
} of total {k}‐dominating functions on G with the property that
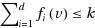 for each v∈V(G), is called a total {k}‐dominating family (of functions) on G. The maximum number of functions in a total {k}‐dominating family on G is the total {k}‐domatic number of G, denoted by
for each v∈V(G), is called a total {k}‐dominating family (of functions) on G. The maximum number of functions in a total {k}‐dominating family on G is the total {k}‐domatic number of G, denoted by
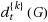 . Note that
. Note that
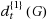 is the classic total domatic number d
t
(G). In this paper we initiate the study of the total {k}‐domatic number in graphs and we present some bounds for
is the classic total domatic number d
t
(G). In this paper we initiate the study of the total {k}‐domatic number in graphs and we present some bounds for
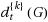 . Many of the known bounds of d
t
(G) are immediate consequences of our results.
. Many of the known bounds of d
t
(G) are immediate consequences of our results.