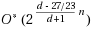| Article ID: | iaor2012240 |
| Volume: | 23 |
| Issue: | 1 |
| Start Page Number: | 94 |
| End Page Number: | 117 |
| Publication Date: | Jan 2012 |
| Journal: | Journal of Combinatorial Optimization |
| Authors: | Bourgeois N, Giannakos A, Lucarelli G, Milis I, Paschos V, Potti O |
| Keywords: | combinatorial optimization |
In this paper, we deal with the problem of finding quasi‐independent sets in graphs. This problem is formally defined in three versions, which are shown to be polynomially equivalent. The one that looks most general, namely,