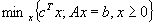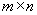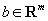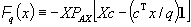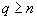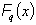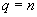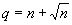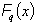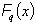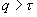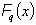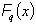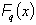| Article ID: | iaor19921535 |
| Country: | United States |
| Volume: | 17 |
| Issue: | 1 |
| Start Page Number: | 225 |
| End Page Number: | 253 |
| Publication Date: | Feb 1992 |
| Journal: | Mathematics of Operations Research |
| Authors: | Monteiro Renato D.C. |
For a possibly degenerate linear program