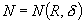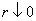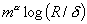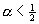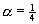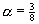A class of algorithms is proposed for solving linear programming problems (with m inequality constraints) by following the central path using linear extrapolation with a special adaptive choice of steplengths. The latter is based on explicit results concerning the convergence behaviour of Newton's method to compute points on the central path 
, and this allows to estimate the complexity, i.e. the total number 
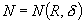of steps needed to go from an initial point 
to a final point 
, by an integral of the local ‘weighted curvature’ of the (primal-dual) path. Here, the central curve is parametrized with the logarithmic penalty parameter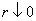 
. It is shown that for large classes of problems the complexity integral, i.e. the number of steps N, is not greater than const 
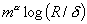, where 
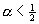e.g. 
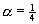or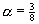 
(not that 
gives the complexity of zero order methods). The authors also provide a lower bound for the complexity showing that for some problems the above estimation can hold only for 
. As a byproduct, many analytical and structural properties of the primal-dual central path are obtained: there are, for instance, close relations between the weighted curvature and the logarithmic derivatives of the slack variables; the dependence of these quantities on the parameter r is described. Also, related results hold for a family of weighted trajectories, into which the central path can be embedded.
