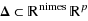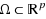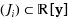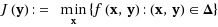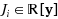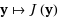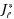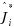Min‐max and robust polynomial optimization

We consider the robust (or min‐max) optimization problem J^*≔maxy∈Ωminx{f(xy):(xy)∈Δ} where f is a polynomial and 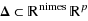$\Delta \subset {ℝ}^{\mathrm{nimes}}{ℝ}^p$ as well as 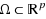$\Omega \subset {ℝ}^p$ are compact basic semi‐algebraic sets. We first provide a sequence of polynomial lower approximations 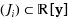$(J_i)\subset ℝ[y]$ of the optimal value function 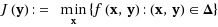$J(y):=\underset{x}{\min }\{f(x,y):(x,y)\in \Delta \}$ . The polynomial 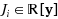$J_i\in ℝ[y]$ is obtained from an optimal (or nearly optimal) solution of a semidefinite program, the ith in the ‘joint + marginal’ hierarchy of semidefinite relaxations associated with the parametric optimization problem 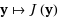$y\mapsto J(y)$ , recently proposed in Lasserre (SIAM J Optim 20, 1995‐2022, 2010). Then for fixed i, we consider the polynomial optimization problem $J_i^{*}:={\max }_y\{J_i(y):y\in \Omega \}$ and prove that ${\hat{J}}_i^{*}(:={\max }_{\ell =1,\dots ,i}{J}_{\ell }^{*})$ converges to J* as i → ∞. 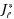Finally, for fixed 𝓁 ≤ i, each $J_{\ell }^{*}$ (and hence 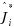${\hat{J}}_i^{*}$ ) can be approximated by solving a hierarchy of semidefinite relaxations as already described in Lasserre (SIAM J Optim 11, 796–817, 2001; Moments, Positive Polynomials and Their Applications. Imperial College Press, London 2009).