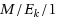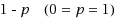Motivated by a congestion problem arising in a Chinese hospital, an
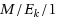queueing system, where the service process is subject to no damage interruptions has been considered. When the first phase of service is completed, the service process can be interrupted with probability
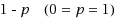as a result of the customer leaving the service area to attend to other work. There is a finite space to accommodate the interrupted customers in the queueing system. When the other work is completed, the customer, whose service was interrupted, will re‐enter the service area and resume his interrupted service based on the non‐preemptive priority rule. Using the matrix geometric method, the steady state behavior of this system is analyzed. Based on the queue length distribution, several important performance measures along with some numerical examples have been discussed. Finally, under a given cost structure, we use the direct search method to determine the optimal capacity of the space to accommodate the interrupted customers.
