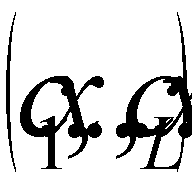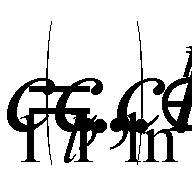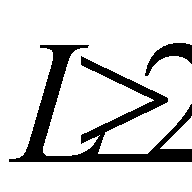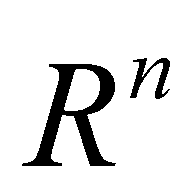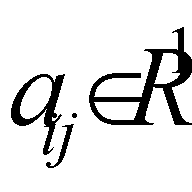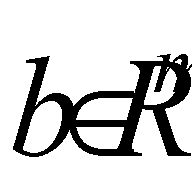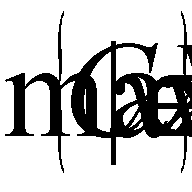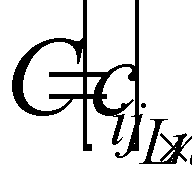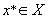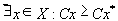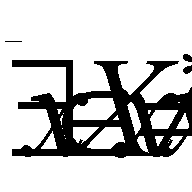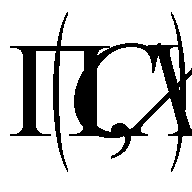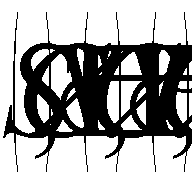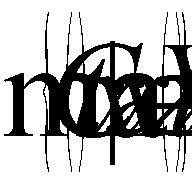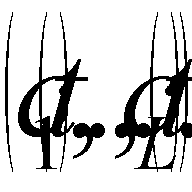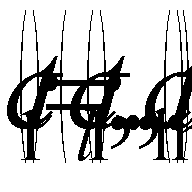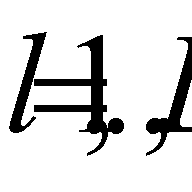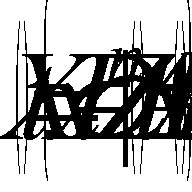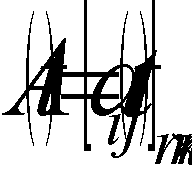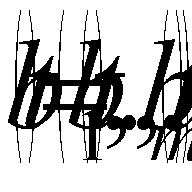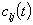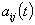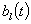Maximize the vector criterion (1)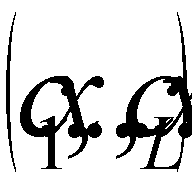 
, which is defined on the set (2) 
, where 
, 
, 
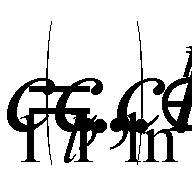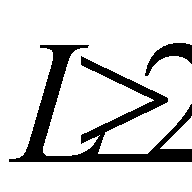, D is a bounded subset of 
, 
,
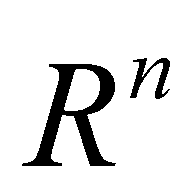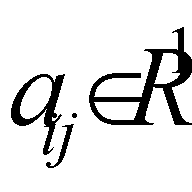and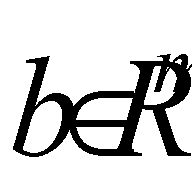 
. The authors also use the following conventional expression for problem (1), (2): 
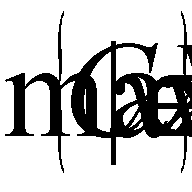, where 
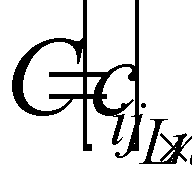. As is known, a point 
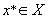is said to be effective (or Pareto-optimal) if 
, 
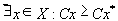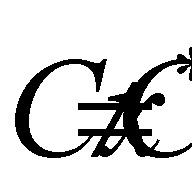; it is said to be weakly effective (semi-effective, optimal in the Slater sense) if 
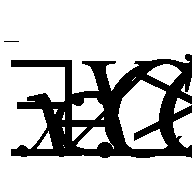, and strictly effective if 
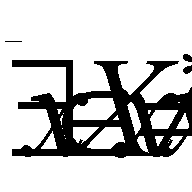. The set of all effective points is denoted by 
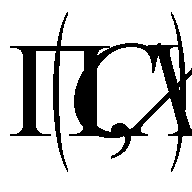, the set of weakly effective points by P(C, X), and the set of strictly effective points by S(C, X). Obviously, 
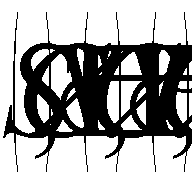. A vector maximization problem usually consists of finding effective points in the set of admissible solutions. Parametric analysis of mathematical programming problems is performed on the basis of models and methods of parameteric programming, the subject of which is optimization problems whose coefficients (all of them or individual ones) are functions of one or more parameters. They propose carrying out a parametric analysis of problem (1), (2) on the basis of the following multicriterial parameter model: 
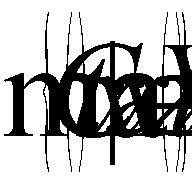, where C(t)=
, 
, 
, 
, 
, 
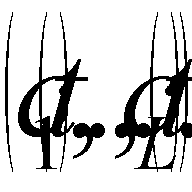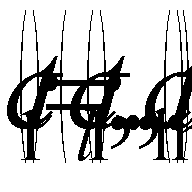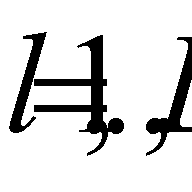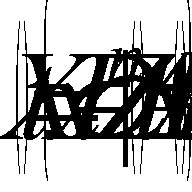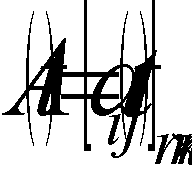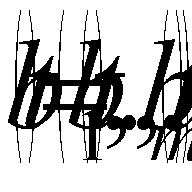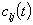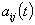, and 
,
and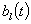 
are real-valued polynomial functions of the parameter 
.
