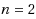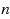| Article ID: | iaor20112913 |
| Volume: | 235 |
| Issue: | 10 |
| Start Page Number: | 3238 |
| End Page Number: | 3244 |
| Publication Date: | Mar 2011 |
| Journal: | Journal of Computational and Applied Mathematics |
| Authors: | Plaza Sergio, Romero Natalia |
| Keywords: | heuristics, heuristics: local search, programming: nonlinear |
We study the relaxed Newton’s method applied to polynomials. In particular, we give a technique such that for any