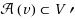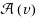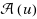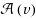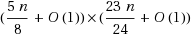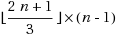Improved floor‐planning of graphs via adjacency‐preserving transformations

Let G=(V,E) and G′=(V′,E′) be two graphs, an adjacency‐preserving transformation from G to G′ is a one‐to‐many and onto mapping from V to V′ satisfying the following: (1) Each vertex v∈V in G is mapped to a non‐empty subset 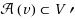$𝒜(v)\subset V\prime$ in G′. 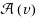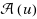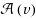The subgraph induced by $𝒜(v)$ is a connected subgraph of G′; (2) if u≠ v∈V, then $𝒜(u)\cap 𝒜(v)=\varnothing$ ; and (3) two vertices u and v are adjacent to each other in G if and only if subgraphs induced by $𝒜(u)$ and $𝒜(v)$ are connected in G′. In this paper, we study adjacency‐preserving transformations from plane triangulations to irreducible triangulations (which are internally triangulated, with four exterior vertices and no separating triangles). As one shall see, our transformations not only preserve adjacency well, but also preserve the endowed realizers of plane triangulations well in the endowed transversal structures of the image irreducible triangulations, which may be desirable in some applications. We then present such an application in floor‐planning of plane graphs. The expected grid size of the floor‐plan of our linear time algorithm is improved to 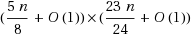$(\frac{5n}{8}+O(1))\times (\frac{23n}{24}+O(1))$ , though the worst case grid size bound of the algorithm remains 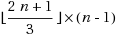$\lfloor \frac{2n+1}{3}\rfloor \times (n‐1)$ , which is the same as the algorithm presented in Liao et al. (J. Algorithms 48:441–451, 2003).