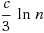In this paper, we study the parameterized complexity of Dominating Set problem in chordal graphs and near chordal graphs. We show the problem is W[2]‐hard and cannot be solved in time n
o(k) in chordal and s‐chordal (s>3) graphs unless W[1]=FPT. In addition, we obtain inapproximability results for computing a minimum dominating set in chordal and near chordal graphs. Our results prove that unless NP=P, the minimum dominating set in a chordal or s‐chordal (s>3) graph cannot be approximated within a ratio of
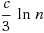in polynomial time, where n is the number of vertices in the graph and 0<c
<1 is the constant from the inapproximability of the minimum dominating set in general graphs. In other words, our results suggest that restricting to chordal or s‐chordal graphs can improve the approximation ratio by no more than a factor of 3. We then extend our techniques to find similar results for the Independent Dominating Set problem and the Connected Dominating Set problem in chordal or near chordal graphs.
