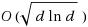In this paper we consider the following closest vector problem. We are given a set of 0–1 vectors, the generators, an integer vector, the target vector, and a nonnegative integer C. Among all vectors that can be written as nonnegative integer linear combinations of the generators, we seek a vector whose 𝓁
∞‐distance to the target vector does not exceed C, and whose 𝓁
1‐distance to the target vector is minimum. First, we observe that the problem can be solved in polynomial time provided the generators form a totally unimodular matrix. Second, we prove that this problem is NP‐hard to approximate within an O(d) additive error, where d denotes the dimension of the ambient vector space. Third, we obtain a polynomial time algorithm that either proves that the given instance has no feasible solution, or returns a vector whose 𝓁
∞‐distance to the target vector is within an
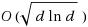 additive error of C and whose 𝓁
1‐distance to the target vector is within an
additive error of C and whose 𝓁
1‐distance to the target vector is within an
 additive error of the optimum. This is achieved by randomly rounding an optimal solution to a natural LP relaxation. The closest vector problem arises in the elaboration of radiation therapy plans. In this context, the target is a nonnegative integer matrix and the generators are certain 0–1 matrices whose rows satisfy the consecutive ones property. Here we begin by considering the version of the problem in which the set of generators comprises all those matrices that have on each nonzero row a number of ones that is at least a certain constant. This set of generators encodes the so‐called minimum separation constraint. We conclude by giving further results on the approximability of the problem in the context of radiation therapy.
additive error of the optimum. This is achieved by randomly rounding an optimal solution to a natural LP relaxation. The closest vector problem arises in the elaboration of radiation therapy plans. In this context, the target is a nonnegative integer matrix and the generators are certain 0–1 matrices whose rows satisfy the consecutive ones property. Here we begin by considering the version of the problem in which the set of generators comprises all those matrices that have on each nonzero row a number of ones that is at least a certain constant. This set of generators encodes the so‐called minimum separation constraint. We conclude by giving further results on the approximability of the problem in the context of radiation therapy.