The linear ordering problem (LOP) is an
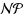‐hard combinatorial optimization problem with a wide range of applications in economics, archaeology, the social sciences, scheduling, and biology. It has, however, drawn little attention compared to other closely related problems such as the quadratic assignment problem and the traveling salesman problem. Due to its computational complexity, it is essential in practice to develop solution approaches to rapidly search for solution of high‐quality. In this paper we propose a new algorithm based on a greedy randomized adaptive search procedure (GRASP) to efficiently solve the LOP. The algorithm is integrated with a Path‐Relinking (PR) procedure and a new local search scheme. We tested our implementation on the set of 49 real‐world instances of input‐output tables (LOLIB instances) proposed in Reinelt (2002). In addition, we tested a set of 30 large randomly‐generated instances proposed in Mitchell (1997). Most of the LOLIB instances were solved to optimality within 0.87 seconds on average. The average gap for the randomly‐generated instances was 0.0173% with an average running time of 21.98 seconds. The results indicate the efficiency and high‐quality of the proposed heuristic procedure.
