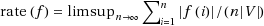Resource‐sharing systems and hypergraph colorings

A resource‐sharing system is modeled by a hypergraph H in which a vertex represents a process and an edge represents a resource consisting of all vertices (processes) that have access to it. A schedule of H=(V,E) is a mapping f:ℕ→2 ^V , where f(i) is an independent set of H which consists of processes that operate at round i. The rate of f is defined as 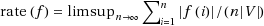$\mathrm{rate}(f)={\mathrm{limsup}}_{n\to \mathrm{\infty }}{\sum }_{i=1}^n\mid f(i)\mid /(n\mid V\mid )$ , which is the average fraction of operating processes at each round. The purpose of this paper is to study optimal rates for various classes of schedules under different fairness conditions. In particular, we give relations between these optimal rates and fractional/circular chromatic numbers. For the special case of the hypergraph is a connected graph, a new derivation for the previous result by Yeh and Zhu is also given.